Ming Gong

Ming Gong

IO小站

1-Memory

18 minute read

Published:

DRAM

Dynamic Random Access Memory: address -> data Content addressable memory: key -> address (Unit 3)

On PCB, DRAM packaged in DIM (Dual Inline Memory Module)

  • Usually 8 chips (9-10 if error correction)
  • Connected to CPU/SOC using the DDR (dual data rate) bus
  • DDR: data can be transferred at both clock edges (double frequency)
    • GDDR: graphics
    • LDDR: low-power
  • DDR5: latest standard
    • Data bus width: 64 bits (32x2)
    • Address bus: 21 bits (Longer addresses take multiple cycles; slow if too wide)
    • Command bus: 7 bits (?)
    • 64 ms refresh
  • DDR Standard: JEDEC, allow different manufactures to interoperate
  • In SOC, the Memory Controller controls the DRAM
    • May have more than 1 MCs
    • Each MC can be attached to more than one DRAM modules
    • The connection DDR is a channel

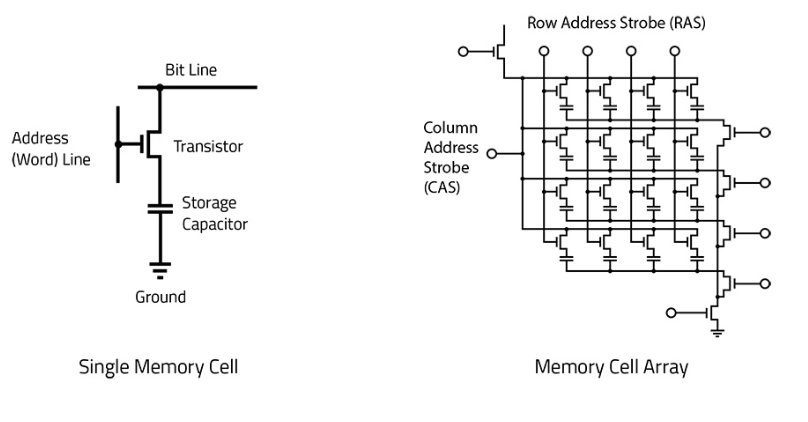
DRAM Cell

G: word line; D: bit line

Write:

  1. Activate word line
  2. bit line = value

Read:

  1. Activate word line,
  2. Discharge value = bit line -> Analog sense amplifier (amplifies to drive)
  3. Take output, and restore the value

Subarray

aka “mats”, square to normalize latency

  • Bit line connected to sense amplifiers
  • Address -> decoder -> word line cell -> subarray -> mat -> sub-bank (~4) -> bank -> chip -> rank -> channel -> DIMM

Bank groups (BG0-7) on a DRAM die

Page buffer in one bank: sense amplifier that holds a data row

  • Each row can be as wide as 8K
  • Refreshing can happen concurrently (other banks can be refreshed while one is read)
  • Any command from processor is broadcasted to all dies

E. DRAM bus runs at 2400 MHz. What is the peak bandwidth between the memory and the SoC?

  • 2400 * 2 * 8 bytes (maximum)

Don’t forget to x2
64-bit: 8 byte per transfer

Commands

REFRESH

  • \(t_{REFI}\): maximum supported refresh interval (~4000 ns)
    • Limits the peak BW
  • \(t_{REFC}\): blocking time for refresh per row (~200 ns)
    • E. about 95% BW available

READ

  • ACT (activate row): drop all data to the bottom buffer on the bank
    • Energizes a particular wordline for subsequent access
    • \(t_{RCD}\) (row-to-column delay) from ACT to CAS
  • CAS (column select)
    • \(t_{CL}\) (column-read delay) for data to be read out
    • Data bursted out then (bursted out in group of 16 (burst length))
  • PRE (precharge): so the next ACT can happen
    • Precharges the row to \(\frac {V_{DD}} 2\) to drive the sense amplifier
    • \(t_{RAS}\) (row-access strobe delay) between PRE to the next ACT
    • If reading a different row in the same bank, \(t_{RP}\) (row-precharge)
      • Not necessary if reading the same row

Error

Soft Error Prone to particle strikes (E. \(\alpha\)), may trigger bit flips

  • Want detect and recover
  • Store data redundantly (E. 2x to detect, 3x to correct)
  • ECC (E. 2D parity)

Hard Error DIM-SOC bus line stuck at 0 all the time

Failure model

FIT: failure of 1 GiB of memory per 1 billion hours of operation

  • ~15 for memory
  • ~100 for GPU memory

SECDED: correct 1-bit faults, detect 2-bit faults

  • Typically done in 64-bit chunks Chip kill: make sure still works if one chip in DIMM fails

Correction Scheme

TMR (Triple Modular Redundancy): give 3 copies to have a majority vote

  • Very cumbersome (3x load latency + comparison; 1/3 capacity)
  • Can correct any number of bit faults

Error Correction Code

  • Sometimes black box
  • Support errors in the check bits
  • Data \(d\) (E. 64 bits) + check code (E. 16 bits)
  • Multiply \(d\) by a constant \(m\). Store \(dm\) in memory
  • When retrieving, divide by \(m\). If no remainder, good;
  • If there’s a remainder \(r\), we know which bit to flip
\[d' = d\times m \pm 2^k\]

where \(k\) is the position of the bit flip To correct,

\[\frac{d'}m = \frac{d\times m}{m}\pm \frac{2^k}m\]

Need to find \(m\) such that \(\frac{2^k}m\) produces unique remainder for all \(k\) (E. 243)

  • Constraint on \(m\): minimize the number of check bits
  • For double error detection, you get a remainder that matches nothing

Error Correction Scrubs (ECS)

Error accumulate over time so you can’t correct

  • Solution: scrub memory periodically
  • Error correction happens in the memory controller: Need to read + write from the chip
  • Also a blocking operation

DDR5 only does SEC (no double-bit) (Q: is it required on thei chip, or ???)

Random Access Strobe timing

\[t_{RAS} = t_{RCD} + t_{CL} + t_{RP}\]

E. DDR5 memory, 1 DIMM on the system, 8 GiB, no ECC, clock 3000 MHz. Estimate the latency of 2 successive (back-to-back) reads to two different rows in the same bank

  • 8 chips on the DIMM, each with 8 Gib of memory; to output 64 bits of data
  • \[t_{RCD} + t_{CL}*n + t_{RP} + t_{RCD} + t_{CL}*n\]
    • Multiple \(t_{CL}\)s that reads burst of data
    • No need for last recharge E2. Same condition, but to the same row
  • \[t_{RCD} + t_{CL}*n + t_{CCD} + t_{CL} * n\]
  • No need \(t_{RP}\) twice
  • \(t_{CCD}\): column-to-column delay E3. Two different banks E4. Two different DIMMs
  • …

Cache

Speed limited by memory

  • Even worst due to instruction fetching (same time as memory access)
  • Store these locally within the SoC in faster memory -> cache

SRAM

Bistable element, with charging capacitor on each side

  • On die
  • Same process technology for memory as with CPU
  • Planar CMOS, trench capacitor

Hierarchy

  • CPU
  • L1I, L1D (L1I -> CPU -> L1D pipeline)
  • L2
  • L3

  • Main memory Each layer has ~10x capacity & access time

  • Temporal locality: loop
  • Spatial locality: array

Physical organization

2D array

  • Line (block) size: 64B
  • x # of cache lines Address -> decoder -> tag array -> data array

When caching address, tag address = x « $log_2$(cache line size)

Associativity

  • Direct mapped: one addresses only map to one index
  • Set associative: one address maps to a set of indices (aka ways). May be in either of it. Decoder checks if either tag in the ways
  • If hit, extract address offset

Policy

Evict policy

  • Random
  • Least recently used item (LRU)
  • Most recently used item (MRU)
  • OPT: relying on a oracle knowledge
  • Adaptive (based on ML algorithms)

Store policy

Hit

  • Write-back: only update L1, mark line dirty
  • Write-thru; Update propagate to higher levels (L2, L3, …)
    • Simple coherence
    • Slow Miss
  • Write allocate: bring data to cache and write
    • Useful for calloc()
    • Good temporal locality
    • Works well with writeback
  • Write around: skip level you miss. Update the level where data hits
    • Useful if no further reuse (E. logging, stream media, free())

Between levels miss (level specific):

  • Inclusive cache: $level_x \subseteq level_{x+1}$. Store in all intermediate level
  • Exclusive cache: a cache line exists uniquely in one level.
    • aka victim caching (evict to next level)
  • NINE: neither, no commitment, in-between

MSHR

Performance optimizations for loads

LD x
LD x+4
LD x+8
LD x+12

Suppose x misses in L1D. Cache Controller issues to L2

  • While L2 is accessing x, processor looks for x+4
    • Wasteful here to issue another miss for x+4
    • Processor fold subsequent misses to the same pending cache line This is called MSHR (Miss Status Handling Registers). Tracks all pending misses
  • Table of missed addresses, corresponding to PC of all subsequent loads
  • One table for each level of cache

HW Table has limited size of the number of addresses, and the number of PCs for each address.

  • If no space, stall CPU (no folding available)

Write Buffer

Performance optimization for store misses

st x 
st x+4
...

Buffer up the stores in a write buffer (mini cache with addresses and 1 line data)

  • Once filled, evicts and sends to the next level. If you load the same address as stored, data forward directly from buffer

Example

Q: How many lookups happen in L2, and how many writes go to the DRAM? L1D MSHR: 4 entries miss[3:0], each can handle 16 misses Suppose load 32K of ints, 64B cache line size

  • First miss instance is stored in a cache line
  • Subsequent misses on the same line are buffered (folded)
  • For L2 layer, need 32K / (4 * 16) = 512 cache line lookups
    • Without MSHR, 64x more
    • 16 * 4 due to 16 fold * 4 bytes for int
      • Exact same as L1D line size, since int is the most common
    • Every 16 misses are collapses into one L2 lookup

L1D store buffer: can combine consecutive writes to 1 cache line

Suppose store 16K ints, 64B cache line size

  • If L1D store miss, send to L2, but not individually
    • Write buffer collects every write into a single cache line st c[15:0] (for int)
    • When line filled, send the request to L2 to write
  • Without store buffer, L2 4096 writes * 4 byte
  • With store buffer, LL2 4096 / 16 = 256 writes * 64 bytes
    • Same data, but less metadata (location, write size, etc.)
  • In L2, still write allocate system -> all misses -> send to DRAM
    • No additional merging possible. All misses are cache line size
  • If you alternate cache writes, st c[i]; st d[i], store buffer will be useless due to conflict

DRAM traffic

  • Memory Controller (MC) that receives all miss traffic from SoC. Makes request (PRE, ACT, column R/W) to DRAM

    Assume

  • 16 GiB DIMM
  • 8 Bank groups (each DRAM is x8, also sending 8 bits of data)
    • Each BG has a row buffer
    • 8 open rows per DRAM
    • 64 open rows per DIMM
  • 4 sub-banks per bank group
  • 2 subchannels per DIMM
  • Miss traffic trace
  • Assume no code misses. Data only
  • Reason from L2 output
read A[0:15]
read B[0:15]   
// still stuck here, but processor will keep requesting
// non-blocking write
read A[16:31]
read B[16:31]
write C[0:15]

Q: How should PA -> DRAM address mapping be set up to improve parallelism

  • Make sure A, B, C need to be written to different banks concurrently
    • If same bank, blocking each other. Won’t need to issue separate open and close
    • E. BG0 has slice of A, BG1 has slice B
  • When MC controlling cache line requests into DRAM commands, process out of order
    • Readings are more critical. Make it happen before the write
    • Instruction page > read > write
    • aka memory scheduling

Cache causality

Reason of misses:

  • Cold (compulsory): first reference
  • Capacity: too small (even if fully associative)
  • Conflict: addresses map to the same cache line
  1. Assume cache is infinitely large and fully associative
    • Any miss will be cold -> label them
    • Solution: pre-load all data into cache (prefetch)
      • Hardware prefetcher (ML-based)
    • Also increase block size
  2. Finite capacity, FA
    • Misses: cold + capacity
    • Solution: increase capacity
  3. Finite capacity, SA/DM
    • Will have everything
    • Subtract the previous two out -> conflict misses
    • Solution: increase associativity
    • change cache indexing (hashing function)
    • change replacement policy
  • Capacity -> latency
  • Block size -> latency (but less extent)
  • Associativity -> latency

Fully associative structure

CAM: content associative memory

  • (tag, data) pairs
  • Search the tag in parallel in every row. If match, data out.
    • Typically 1 clock cycle
    • Number of items searched in 1 cycle: search scope of a scan
    • XNOR check every bit of the tag -> every bit ANDed
    • The key bits are broadcasted to every cell -> latency increases very rapidly

PORT

How many R/W can do to a given memory at a time

  • E. 1R1W; 1RW; 2R1W
  • 1RW: standard SRAM array. Only one address (wordline) you can energize
  • 2R: additional wordline and bitlines attached to every cell. Two sets of sense amplifiers. To transistors controlling the read -> more latency

Example:

  • RF: 2nR, nW (n is the number of concurrent instructions in-flight)
  • L1: 2R, 1W
  • L2: 1RW

HW1

  • clflush(ra): evict from cache block. If cache line is 64 bytes, need to do for all ra % 64
  • rdtsc: timer, issued before and after
    • Need to serialize the instructions
    • Use rdtscp
    • Or insert cpuid just before the rdtsc
    • lfence
  • mfence: prevent multiple CPU cores to interact with memory at the same time Noise reduction techniques:
  • Pin process to specific cores: taskset
  • Pin certain page for DRAM: mlock

Virtual Memory

Very large linear array, abstraction. Allow portable code

  • 0 to \(2^N-1\).
  • The next location is previous location + 1
  • Not all physically addressable

Caching

How to provide such VM illusion Physical memory = populated DRAM (~GB) + size of swap space (E. SSD, HDD, tape ~TB) Solution: cache VM chunks into physical memory Raises a few questions

  • Block size? page size (OS page size, not to be confused with DRAM row buffer size)
    • In modern OS, 4 kB, 1 MB, 2 MB, 1 GB
  • Associativity? fully associative
    • When malloc() called, a chunk is allocated and mapped to the DRAM page
      • Allocates anonymous data. Not stored to hard drive
      • After certain malloc()s, DRAM fill out. Moved to swap space
      • If swap space also fills up: Out Of Memory (OOM). Can no longer illusion
    • For file-backed data reading, resides on non-volatile storage
      • Placed in DRAM page cache when read
    • If miss in DRAM, swap space fetch cost is very expensive. Associativity reduced conflict misses.
      • Search is done in software (OS)
    • Can’t do FA for lower-level cache, since hardware algorithms for searching data can’t execute in ns.
  • Eviction policy?
  • Store hit policy? exclusive between swap space and DRAM
    • Except page cache in DRAM is inclusive (caches hard drive files)
      • Flush command pushes page cache to hard drive
    • For anonymous data, DRAM is the final destination
  • Store miss policy? write allocated to DRAM

This is called software managed cache

  • Replacement in SW (higher latency)
  • Fully associative

Page Table

Data and metadata (ana tag)

  • Page address
  • Permission (rwx)
  • WC (does it support multiple consecutive writes)
  • UC (uncacheable)
  • User/kernel Need to know which pages are present in DRAM + Swap

Data structure: page table Need to

  • Locate item quickly (E. n-ary tree)
  • allocate/deallocate pages
  • Small in size

Page walk

aka search through the tree for address translation

  • Implemented in HW or SW

    E. if tree has 5 levels, need 5 reads to get a memory address.

TLB

Cache page walks -> Translation Lookaside Buffer

  • Special cache for VA -> PA pairs
  • Same level as L1
  • One page walk done, cached to TLB

VM cannot be directly mapped to cache, since different programs will have different VA. Need to first translate to PA

  • Can directly translate if sure that PA not used by any other addresses Program -> VA -> PA (page walk, TLB cached, else expensive) -> cache
  • TLB latency + cache latency
  • 50% overhead :(

VIPT

Optimization: given VA, lookup in TLB and cache concurrently

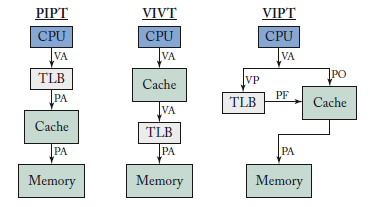
VIPT caches (Virtually Indexed Physically Tagged)

  • Virtual address to compute index
  • Physical address to check tag
  • Need VA -> PA to conserve index & offset bits
  • \(log_2\)(page size) = index + offset bits

Translation overhead

  • PA only: embedded system
    • If you know exactly how many processes the system has.
    • No dynamism
  • Page table
    • High radix structure (tree) to optimize the search
    • 4-5x overhead!
  • Cache VA -> PA translation in TLB
    • Virtual page number -> physical page number
    • Only pay cost once
    • TLB is fully associative, since misses are very expensive
  • VIPT: hide TLB lookup latency under cache latency
    • Virtual page numbercache indexcache offset

Optimizations

Cache size limited by page offset bits. Suboptimal Solution: make cache set associative, so each index can store multiple tags

  • Allows larger total cache size for same index bits
  • If TLB miss, raise an exception (TLB fault), handled by OS or hardware microcode
    • Page walk, and fill in TLB
    • Build HW caches for each page walk level (again)
      • Known as MMU caches
  • If no translation exists (first-time access): page fault

Example

Virtual -> physical -> cache -> DRAM

int *a = malloc(4096 * sizeof(int));  // dynamically allocated
// same for b and c
c[i] = a[i] + b[i];

Suppose 64-bit VA space, 40-bit PA space -> $2^{40}$ max DRAM capacity

  • OS page size: 4 KiB

Max page

  • Max working set size (data only) = 3 * 4096 * 4B= 48 KiB -> 12 page table entries
  • malloc() will align to page entries
    • .align compiler command

Physical Config

Suppose:

  • L1D: 64 k, 64 B lines x 64 sets x 16 ways
  • L2D: 256 KiB, 64 B lines x 16k
  • L3: 8 MiB, 64 B lines
  • Writeback for hit, write around for miss
  • 4 KiB page size
  • VIPT

Q: What is the size of the L1D tag array, assuming a VIPT cache - Page size = 64B x 64 sets = 4K - 40-6-6=28 bits of tag (use physical size) for each line - Total: 28 bits * (64 sets * 16 ways)

  • Assume a FA, 16-entry TLB
    • TLB is 1 valid bit + VPN tag + PPN tag
    • Size of one entry = 1 + (64-12) + (48-12) = 69 bits
  • If TLB includes the bits used from MRU replacement,
    • 4 bits of index for MRU entry, 4 more bits
  • If include LRU replacement,
    • 4 bits for each MRU entry, 16 more bits
    • OR a matrix with comparison bits for each entry: 16 * 15 / 2
      • More data, but simpler comparison algorithm

Code Optimization

To improve locality E. A 2D (byte) matrix is laid out linearly in memory

  • Load The bae address
  • Add offset (0)
  • Store this address to somewhere else in memory With cache (E. 4-entry, FA cache, line size: 4B, writeback on store hit, write allocate on store miss)

Suppose transposing a matrix, row accesses will hit, but column ones will miss

  • Memories are in row-major order, so the columns will miss!
  • Change how arrays are accessed, and increase
  • Fetch a square block of data into the cache -> Cache blocking
    • Set up loop index, so the amount of data accessing fits into the cache size

You May Also Enjoy

Demystifying Cache—From Bytes to Tags

7 minute read

Published:

Breaking down cache address bits is tricky. In this guide, we’ll step through in detail how to partition a 32-bit address and work through some problems to test your understanding :)