So What Is Carry Look Ahead
Published:
Someone asked me about carry lookahead during OH, and I felt that I didn’t explain it well enough. Here’s a better attempt:
The Problem: Waiting for the Carry
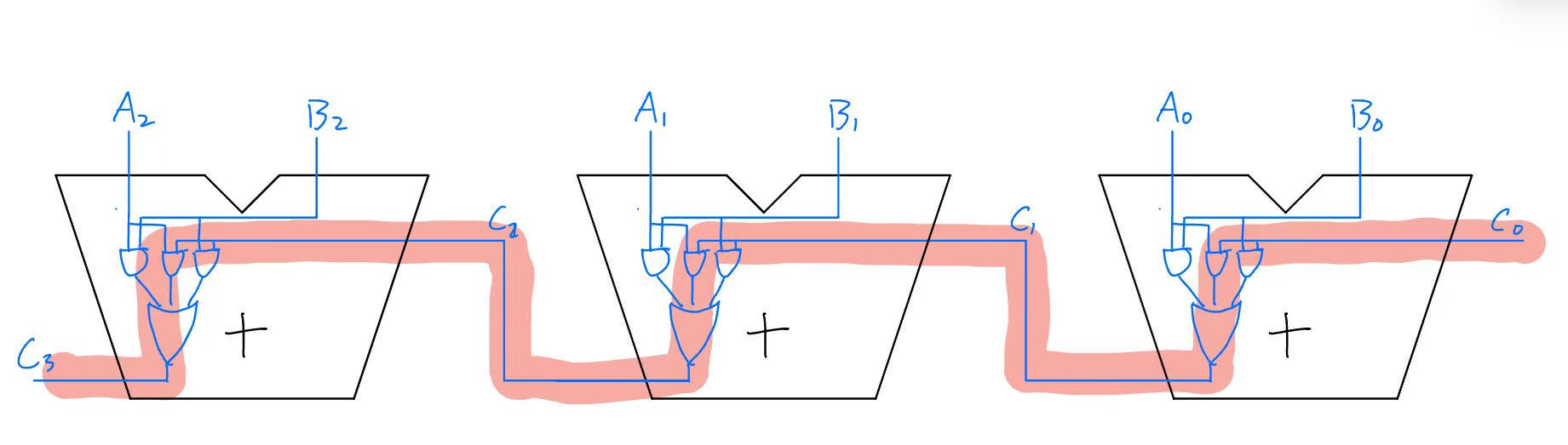
Imagine adding two numbers by hand. You start from the rightmost digit and move left. If one column adds up to 10 or more, you carry a 1 to the next column. This is how basic adders work—the carry-in (Cin) of each bit depends on the carry-out (Cout) of the previous bit. This creates a critical path that spans all previous adders, making it slow.
The Solution: Thinking Ahead
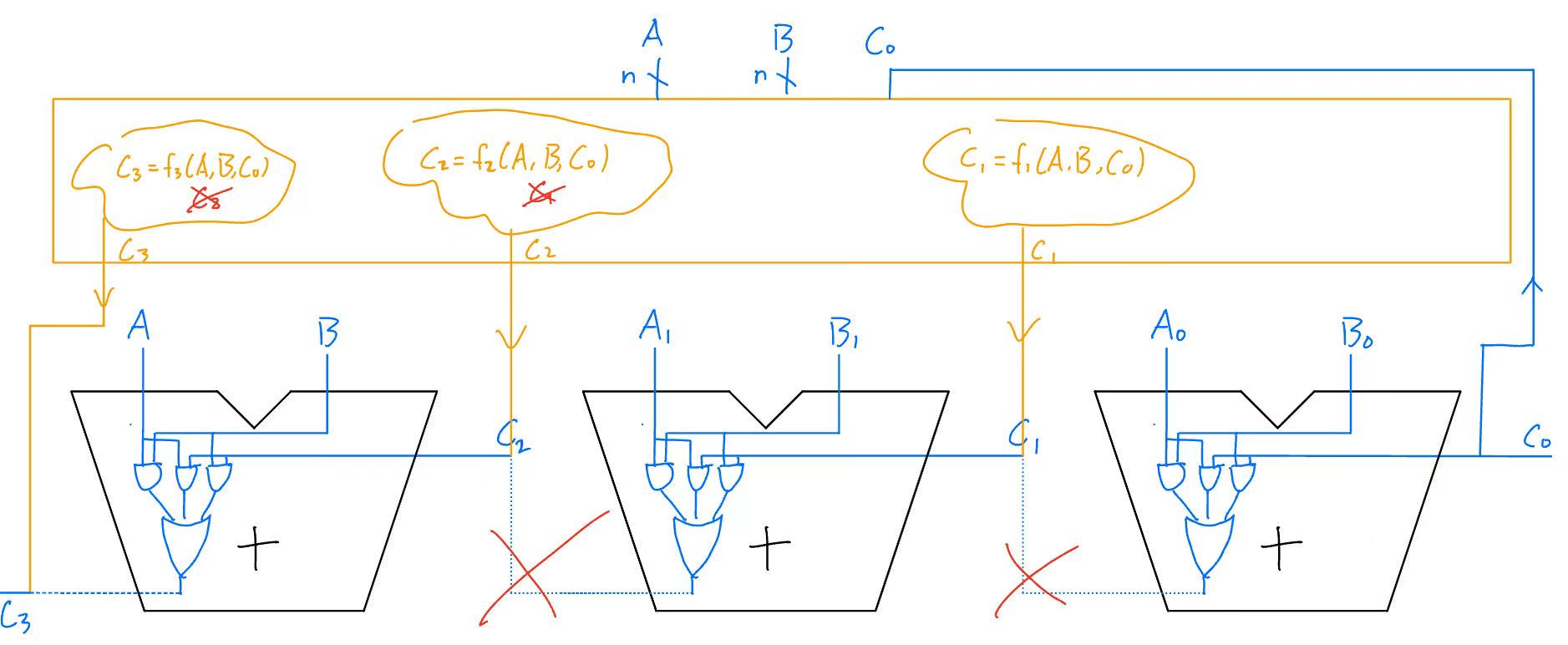
However, addition is purely combinatorial logic, meaning we should be able to express the final carry (Cn) directly in terms of the inputs A and B, without waiting for previous carries. Carry lookahead does exactly that by computing carries in parallel directly from the inputs, instead of sequentially. The formula is:
\[C_{i+1} = G_i + C_iP_i\]Generate (\(G_i\)): If both numbers in a column are 1s, a carry must happen no matter what. (\(G_i = A_iB_i\))
Propagate (\(P_i\)): If at least one of the numbers is 1, a carry might happen if there was a carry (\(C_i\)) from before. (\(P_i = A_i + B_i\))
Now each carry bit depends only on the inputs, not on previous carries. We effectively decoupled the carry propagation.
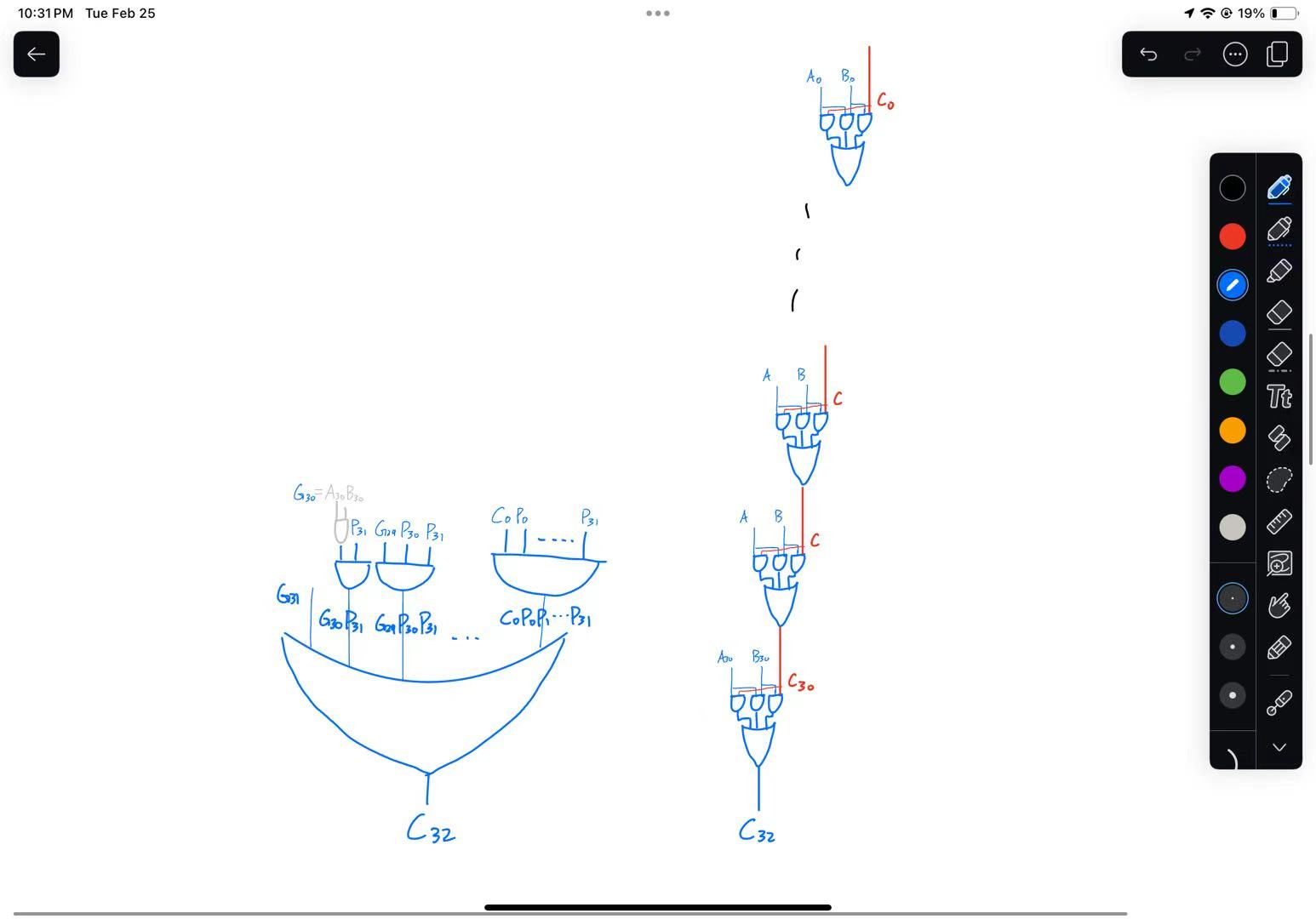
Why this is faster
Consider a 32-bit adder. The final carry bit is:
\[C_{32} = G_{31} + C_{31}P_{31}\] Multiply it out (try it on \(C_3\) first, and you’ll find this amazing pattern):
\[G_{31} + G_{30}P_{31} + G_{29}P_{30}P_{31} + ... + G_0 P_1 P_{30} P_{31} + C_0 P_0 P_1 ... P_{30} P_{31}\]Looks incredibly complicated, right? It’s okay if you don’t fully get the algebra. But overall, this reduces to just two main layers. Each layer involves at most \(n+1\) terms. Since an \(n\)-input AND gate can be represented by \(log_2(n)\) levels of 2-input AND2 gates (how?), the computation is much faster.